Duality and Isomorpism I
by makoMako and QwenMath
好的,我们来深入探讨对偶空间 (Dual Space)、对偶原理 (Duality Principle)、同构 (Isomorphism) 和自然同构 (Natural Isomorphism) 这几个在现代数学中至关重要的概念。我会从多个层次为你剖析,并揭示它们之间深刻的联系。
核心概念概览
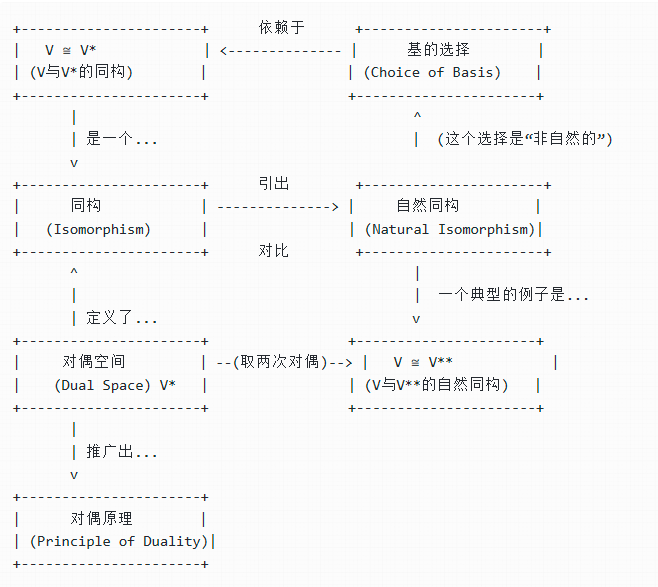
为了建立一个清晰的知识框架,我们可以用一张图来描绘这几个概念的关系:
1. 对偶空间 (The Dual Space)
对偶空间是线性代数中最基本的构造之一,它将“向量”和“作用于向量的线性函数”联系起来。
层次 1:直观理解 —— “测量”的空间
想象一个三维空间 $V = \mathbb{R}^3$ 中的向量,例如 $v = (x, y, z)$。我们可以用不同的方式“测量”这个向量。例如:
- 测量它的 x 坐标。
- 测量它的 y 坐标。
- 测量它的 x 和 y 坐标之和。
这些“测量”操作,如果它们是线性的,就可以被看作是对偶空间中的元素。一个线性测量(或线性函数)$f: V \to F$(其中 $F$ 是标量域,如 $\mathbb{R}$)必须满足:
- $f(v+w) = f(v) + f(w)$
- $f(c \cdot v) = c \cdot f(v)$
例如,定义 $f_1(x, y, z) = x$,这是一个线性函数。定义 $f_2(x, y, z) = 2x + 3y - z$,这也是一个线性函数。而 $g(x, y, z) = x^2$ 就不是线性的。
对偶空间 $V^*$ 就是所有这些线性“测量”或“线性函数”构成的集合。
层次 2:形式化定义
给定域 $F$ 上的一个向量空间 $V$,其**对偶空间(Dual Space),记作 $V^*$,是所有从 $V$ 到 $F$ 的线性映射(这些映射也称为线性泛函(linear functionals)*)的集合。
$$V^ = { f: V \to F \mid f \text{ is a linear map} }$$
$V^*$ 本身也构成一个向量空间,其上的加法和标量乘法定义如下:
- 加法: $(f+g)(v) = f(v) + g(v)$
- 标量乘法: $(c \cdot f)(v) = c \cdot f(v)$
其中 $f, g \in V^*, v \in V, c \in F$。
层次 3:对偶基 (The Dual Basis)
如果 $V$ 是有限维的,且有一组基 $\mathcal{B} = {e_1, e_2, \dots, e_n}$,那么其对偶空间 $V^*$ 也一定有一组与之对应的基,称为**对偶基 (Dual Basis)**,记作 $\mathcal{B}^* = {e^1, e^2, \dots, e^n}$。
这组对偶基的定义非常巧妙,第 $i$ 个对偶基向量 $e^i$ 的作用是“提取”原空间中任意向量在基向量 $e_i$ 上的分量。它的形式化定义是:
$$e^i(e_j) = \delta^i_j = \begin{cases} 1 & \text{if } i=j \ 0 & \text{if } i \neq j \end{cases}$$
这里 $\delta^i_j$ 是克罗内克符号 (Kronecker delta)。
重要推论:如果 $V$ 是 $n$ 维的,那么它的对偶空间 $V^*$ 也是 $n$ 维的。即 $\dim(V) = \dim(V^*)$。
2. 同构 (Isomorphism)
这个概念是连接 $V$ 和 $V^*$ 的桥梁。
层次 1:直观理解 —— “结构完全相同”
在数学中,“同构”意味着两个数学结构(如群、环、向量空间)在所有结构性质上都是无法区分的。它们仅仅是元素的“名字”不同而已。对于向量空间而言,如果两个空间同构,那么它们作为向量空间的一切行为(线性组合、线性无关、维数等)都是一样的。
层次 2: 形式化定义
两个向量空间 $V$ 和 $W$ 称为同构 (isomorphic),记作 $V \cong W$,如果存在一个双射(既是单射又是满射)的线性映射 $T: V \to W$。这个映射 $T$ 称为一个同构映射。
核心结论:两个有限维向量空间同构的充要条件是它们的维数相等。
层次 3:$V$ 与 $V^*$ 的同构关系
因为对于有限维向量空间 $V$,我们有 $\dim(V) = \dim(V^*)$,所以我们立刻可以得出结论:
$$V \cong V^*$$ 也就是说,一个有限维向量空间和它的对偶空间是同构的。我们可以通过选择一组基 ${e_i}$ 和其对偶基 ${e^i}$ 来构造一个同构映射 $T: V \to V^*$,定义为 $T(e_i) = e^i$,然后线性地扩展到整个空间。
但是,这个同构存在一个深刻的问题,它引出了我们下一个概念。
3. 自然同构 (Natural Isomorphism)
自然同构是一种“更好”的同构,它不依赖于任何任意的选择(如基的选择)。
层次 1:直观理解 —— “不依赖于坐标系的对应关系”
我们刚刚建立的 $V \cong V^*$ 的同构映射依赖于我们选择的基。如果你换一套基,你就会得到一个完全不同的同构映射。这就像在两个国家间翻译地址,如果翻译规则依赖于你选择的某个特定城市作为“原点”,那么这个规则就不够“自然”。我们希望找到一个不依赖于任何特定选择的、普适的对应关系。
层次 2:形式化定义 —— 双对偶 (The Double Dual)
让我们考虑对偶空间的对偶空间,称为**双对偶空间 (Double Dual Space)**,记作 $V^{**} = (V^*)^*$。它是 $V^*$ 上所有线性泛函构成的空间。
对于有限维空间,我们有 $\dim(V) = \dim(V^*) = \dim(V^{**})$。因此,$V$ 和 $V^{**}$ 也是同构的。但这次,我们可以构造一个不依赖于基的、非常“自然”的同构映射。
这个自然同构映射通常记为 $\Phi: V \to V^{**}$,它的定义如下:
对于 $V$ 中的任意一个向量 $v$,我们将其映射到 $V^{**}$ 中的一个元素 $\Phi(v)$。而 $\Phi(v)$ 本身是一个作用于 $V^*$ 的线性泛函。我们定义 $\Phi(v)$ 的作用是:$$
\Phi(v)^1(f) = f(v) \quad \text{for all } f \in V^*
$$ 这个映射 $\Phi(v)$ 通常也被称为**求值映射 (evaluation map)**,记作 $\text{ev}_v$。所以上式也可以写成 $\text{ev}_v(f) = f(v)$。
为什么这个映射是“自然的”?
请仔细观察这个定义:$\Phi(v)^1(f) = f(v)$。
在它的定义中,我们没有用到任何关于基、坐标或其他任意选择的信息。它只用到了向量 $v$ 和泛函 $f$ 的配对(即“泛函作用于向量”这一基本操作)。无论你如何选择基,这个映射 $\Phi$ 的定义保持不变。
可以证明,对于有限维向量空间,这个映射 $\Phi$ 是一个同构。
层次 3:范畴论视角 (Category Theory Perspective)
在范畴论的语言中,“自然性”有严格的定义。一个自然同构是两个函子 (Functor) 之间的一个同构的自然变换 (Natural Transformation)。
- 考虑恒等函子 $Id: \textbf{Vect}_F \to \textbf{Vect}_F$,它将每个向量空间映射到其自身。
- 考虑双对偶函子 $(\cdot)^{**}: \textbf{Vect}_F \to \textbf{Vect}_F$,它将每个向量空间 $V$ 映射到其双对偶 $V^{**}$。
我们之前定义的映射 $\Phi$ 实际上是一个自然变换 $\Phi: Id \to (\cdot)^{**}$。因为对于任何有限维向量空间 $V$,分量 $\Phi_V: V \to V^{**}$ 都是一个同构,所以 $\Phi$ 是一个自然同构。
而 $V$ 与 $V^*$ 之间不存在这样的自然同构。任何试图建立 $V$ 与 $V^*$ 之间同构的尝试,最终都会发现它无法满足自然变换的交换图要求,因为它总是与基的选择纠缠在一起。
总结:
- 同构$V \cong V^*$:存在,但依赖于基的选择。它是“非自然的”。
- 自然同构$V \cong V^{**}$:存在,且不依赖于任何选择。它是“自然的”、“典范的”(canonical)。
这个区别在处理无穷维空间时尤为重要。在无穷维情况下,$V$ 到 $V^{**}$ 的自然映射 $\Phi$ 仍然是单射,但通常不是满射,因此 $V$ 只是 $V^{**}$ 的一个子空间。
4. 对偶原理 (Principle of Duality)
对偶原理是建立在对偶空间概念之上的一种深刻的哲学思想和证明技巧。
层次 1:直观理解 —— “定理的镜像版本”
对偶原理指出,对于任何关于有限维向量空间中子空间、维数、基等属性的定理,都存在一个“对偶版本”的定理。这个对偶定理可以通过系统地将概念替换为其对偶概念来得到。
例如:
- 概念“向量 $v$” 的对偶是 “线性泛函 $f$”。
- 概念“子空间 $W \subseteq V$” 的对偶是 “歼灭子 (annihilator) $W^0 \subseteq V^*$”。
- 概念“包含关系 $W_1 \subseteq W_2$” 的对偶是 “反向的包含关系 $W_2^0 \subseteq W_1^0$”。
层次 2:一个具体的例子
考虑一个定理:设 $V$ 是有限维向量空间,$U, W$ 是其子空间,则:
$$
\dim(U+W) = \dim(U) + \dim(W) - \dim(U \cap W)
$$利用对偶原理,我们可以推导其对偶版本。关键的对偶关系是:
- $(U+W)^0 = U^0 \cap W^0$
- $(U \cap W)^0 = U^0 + W^0$
- $\dim(S^0) = \dim(V) - \dim(S)$ 对于任意子空间 $S$。
将这些关系代入维数公式,经过一番推导,你会发现你最终证明了原始的公式。更重要的是,任何一个只涉及子空间、交、和、维数的定理,都可以通过这种方式“翻译”成另一个有效的定理。
层次 3:证明的对称性
对偶原理的深刻之处在于$V$和$V^{**}$之间的自然同构。因为 $V \cong V^{**} $ 是自然的,所以任何关于 $V$ 的内在结构定理,都可以通过这个自然同构“传递”到 $ V^{**} $ 上。而 $V^{**}$ 是 $V^*$ 的对偶空间。
这意味着,一个关于“向量空间和其子空间”的陈述,可以被翻译成一个关于“对偶空间和其子空间”的陈述。证明一个,就等于证明了另一个。这为数学证明提供了强大的对称性和经济性。
总结与关系梳理
- 对偶空间 ($V^*$) 是基础。它为我们提供了一个与原空间 $V$ 紧密相关但又不同的新空间,由所有线性测量组成。
- 由于有限维时 $\dim(V) = \dim(V^*)$,我们知道它们是同构的。这是一种“存在性”的结论,但具体的同构映射是人为选择的,因而是“非自然的”。
- 为了寻找一种不依赖于人为选择的同构,我们构造了双对偶空间 $V^{**}$。我们发现存在一个从 $V$ 到 $V^{**}$ 的自然同构,这个映射的定义方式是普适的、典范的。
- $V \cong V^{**}$ 的自然性是对偶原理的理论基石。它保证了 $V$ 和 $V^*$ 之间的关系具有深刻的对称性,使得关于一个空间的定理可以系统地转化为关于另一个空间的定理。
简单来说,从 $V$ 到 $V^*$,我们看到了一个依赖于选择的“镜像”。而从 $V$ 到 $V^{**}$,我们看到了一个不依赖于选择的、完美的“自身反射”。正是这种完美的自身反射,赋予了对偶理论强大的威力。
深度阅读建议
- Sheldon Axler, Linear Algebra Done Right: 这本书在不引入行列式的情况下,非常优雅地处理了对偶空间和泛函,对理解其本质非常有帮助。
- Serge Lang, Linear Algebra: 经典的教材,对对偶空间和多重线性代数有非常清晰的介绍。
- nLab (ncatlab.org): 如果你想从范畴论的最高视角来理解自然性 (naturality) 和对偶性 (duality),nLab是最好的在线资源之一。可以搜索 “dual vector space”, “natural transformation”。
- Math Stack Exchange: 搜索 “natural vs. canonical isomorphism”, “duality principle linear algebra” 等关键词,可以找到大量高质量的讨论,提供了多种不同的理解角度。
