Duality and Isomorpism IX
当然!对偶和同构是数学中最富诗意和启发性的思想之一。它们像一面面魔法镜子,能在一个数学对象的“镜像”中发现其深刻的、未曾预料到的性质。下面是一些来自不同数学领域的、妙趣横生的例子。
1. 几何学的诗篇:点与线的对偶 (Projective Duality)
这是最经典、最直观的对偶范例。
- 领域: 射影几何 (Projective Geometry)
- 核心思想: 在二维射影平面上,“点”和“线”的地位是完全对等的。任何关于点和线的定理,只要将“点”和“线”互换,将“经过”和“包含”互换,就能得到一个新的、同样成立的定理。
直观解释:
欧几里得几何中有个小麻烦:不是任意两条直线都相交(平行线是个例外)。射影几何通过引入“无穷远点”和“无穷远直线”修复了这个问题。在这个完美的世界里:
- 公理1: 任意两个不同点,都确定唯一一条直线。
- 公理2: 任意两条不同直线,都相交于唯一一个点。
请看这两条公理的完美对称性!它们就是互为对偶的。我们可以建立一个“对偶词典”:
| 原始概念 | 对偶概念 |
|---|---|
| 点 (Point) | 直线 (Line) |
| 一条直线经过一个点 | 一个点在一条直线上 |
| 共线的点 (Collinear points) | 共点的线 (Concurrent lines) |
| 连接两点的直线 | 两条直线的交点 |
妙趣之处 (The “Aha!” Moment):
这个对偶性意味着,你每证明一个定理,就等于免费证明了它的对偶定理。
- 帕斯卡定理 (Pascal’s Theorem): 如果一个六边形的六个顶点都在一个圆锥曲线(如椭圆)上,那么三对对边的交点是共线的。
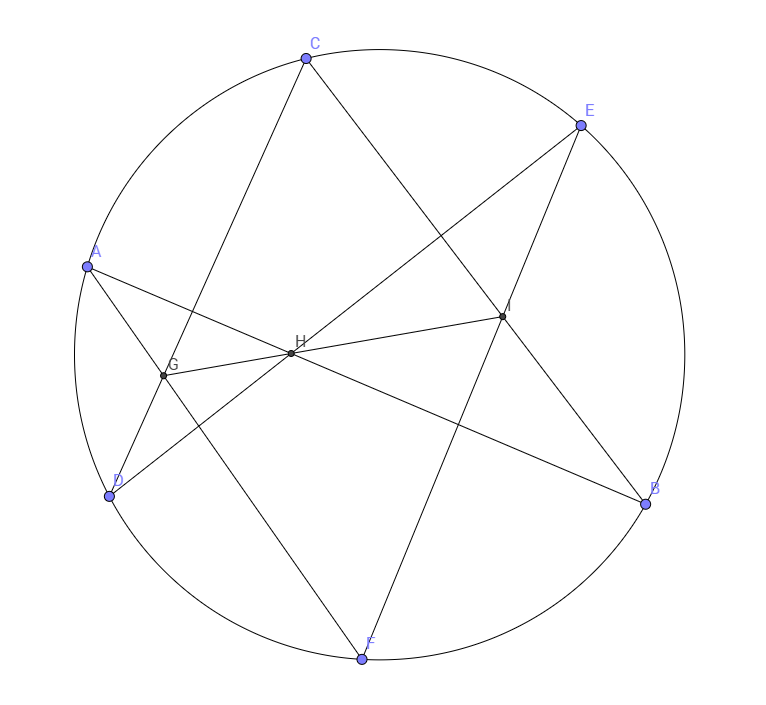
- 布列安桑定理 (Brianchon’s Theorem): 如果一个六边形的六条边都与一个圆锥曲线相切,那么三条对角线(连接对顶点的线)是共点的。
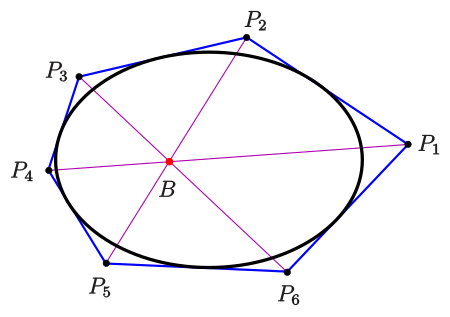
这两个看起来截然不同的定理,实际上是同一个定理的两个对偶版本。证明了其中一个,另一个自动成立。这是数学对称性之美的极致体现。
2. 图论的镜像:平面图对偶 (Planar Graph Duality)
- 领域: 图论 (Graph Theory)
- 核心思想: 任何一个画在平面上且没有边相交的图(平面图),都有一个与之对应的“对偶图”。原图的“面”变成了对偶图的“点”。
直观解释:
给定一个平面图 $G$,我们可以这样构造它的对偶图 $G^{\ast}$:
- 在 $G$ 的每一个面(包括外部无限大的面)里放一个点,这些点就是 $G^{\ast}$ 的顶点。
- 如果 $G$ 中有两个面被一条边 $e$ 分隔,那么就在这两个面对应的 $G^{\ast}$ 顶点之间连一条边 $e^{\ast}$,这条边要穿过原来的边 $e$。
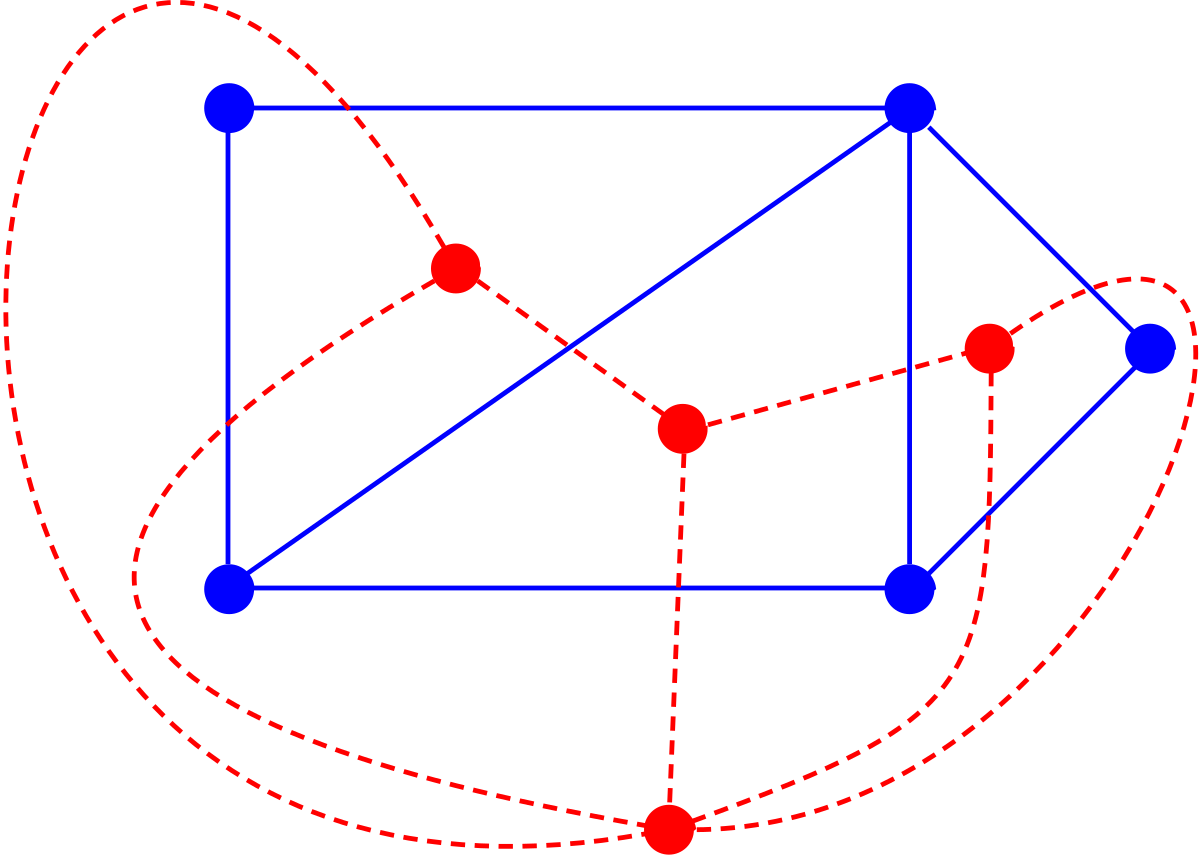
对偶词典:
| 原图 G 的概念 | 对偶图 G* 的概念 |
|---|---|
| 面 (Face) | 顶点 (Vertex) |
| 边 (Edge) | 边 (Edge) |
| 顶点 (Vertex) | 面 (Face) |
| 环 (Cycle) | 割 (Cut-set) |
妙趣之处:
- 欧拉公式的自我对偶: 著名的欧拉公式指出,对于任何连通平面图,$V - E + F = 2$(顶点数 - 边数 + 面数 = 2)。当你把它应用到对偶图 $G^{\ast}$ 时,根据词典,$V^{\ast} = F, E^{\ast} = E, F^{\ast} = V$。所以公式变成 $F - E + V = 2$,这和原公式是完全一样的!这个深刻的公式本身就是自对偶的。
- 最短路与最大流: 在某些网络流问题中,在一个图上寻找最大流的问题,等价于在其对偶图上寻找最短路的问题。这是运筹学中一个非常深刻且有用的结论。
3. 分析的乐谱:傅里叶变换 (Fourier Transform)
- 领域: 谐波分析 (Harmonic Analysis)
- 核心思想: 傅里叶变换建立了一个函数空间与它自己的对偶空间之间的一种同构。它将一个函数(通常看作是“时域”或“空域”信号)与它的频谱(“频域”信号)对应起来。
直观解释:
想象一段音乐。我们可以把它看作是随时间变化的声波压力(时域信号),这是函数 $f(t)$。傅里叶变换就像一个棱镜,能将这段复杂的声波分解成一系列纯粹的音高(正弦波)的叠加,告诉我们每个音高(频率)的强度有多大。这个频率强度的分布就是频谱,即函数 $\hat{f}(\omega)$。
- 傅里叶变换: $$ \hat{f}(\omega) = \int_{-\infty}^{\infty} f(t) e^{-2\pi i \omega t} \mathrm{d}t $$
- 傅里叶逆变换: $$ f(t) = \int_{-\infty}^{\infty} \hat{f}(\omega) e^{2\pi i \omega t} \mathrm{d}\omega $$
这两个变换公式几乎长得一模一样(只有一个符号的差别),这暗示了一种深刻的自对偶性。
对偶的体现:
- 时域与频域的对偶: 函数空间与它的频谱空间互为对偶。
- 性质的对偶:
- 一个在时域上非常窄的信号(比如一声短促的击掌),其频谱在频域上一定非常宽(包含了各种频率的成分)。
- 一个在频域上非常窄的信号(比如一个纯净的音叉声,频率单一),其波形在时域上一定非常宽(理论上无限延伸)。
妙趣之处 (海森堡不确定性原理):
物理学中的海森堡不确定性原理,说的是我们无法同时精确地知道一个粒子的位置和动量。这在数学上,正是傅里叶变换对偶性的直接推论!
将粒子的波函数看作是 $f(x)$(位置空间),其动量分布就是它的傅里叶变换 $\hat{f}(p)$(动量空间)。
- $\Delta x$(位置的不确定性)衡量了 $f(x)$ 的“宽度”。
- $\Delta p$(动量的不确定性)衡量了 $\hat{f}(p)$ 的“宽度”。
傅里叶分析中的一个基本定理(有时就叫不确定性原理)指出:
$$ \Delta x \cdot \Delta p \ge \frac{\hbar}{2} $$
这个在量子力学中如此神秘的原理,其数学本质就是一个函数和它的傅里叶变换的“宽度”之积不可能无限小。这完美地展示了抽象的对偶思想如何解释了物理世界的基本法则。
4. 拓扑学的灵魂:庞加莱对偶 (Poincaré Duality)
您描述的甜甜圈表面(a torus, $T^2$)的性质,以及其“洞”和“切割”的概念,是代数拓扑学(Algebraic Topology)中非常经典且直观的例子,尤其是在讲解同调(Homology)、上同调(Cohomology) 和 庞加莱对偶性(Poincaré Duality) 时。
这个形象化的描述本身很难追溯到一个唯一的“出处”,因为它是一种教科书般通用的解释方式。您可以在几乎所有关于代数拓扑的入门书籍或课程中找到类似的阐述。例如,经典的教材如 Allen Hatcher’s “Algebraic Topology”(尤其是关于同调和流形的部分)会对这些概念有详细的数学定义和解释,尽管不一定会用完全相同的口头化表述。
以下将详细解释提到的概念以及庞加莱对偶性。
1. 甜甜圈表面 (Torus, $T^2$) 的拓扑性质

您对甜甜圈表面“洞”的描述是完全正确的,它完美地概括了其同调群(Homology Groups)的性质:
1维的洞 (1-dimensional holes / cycles):
在拓扑学中,我们用**同调群(Homology Groups)来量化“洞”的概念。对于一个$n$-维的对象,其$k$-维同调群 $H_k(M)$ 描述了其$k$-维的不可收缩的“循环”(cycles)**的数量(更准确地说,是它们的基)。- 对于甜甜圈表面 ($T^2$),有两个独立的1-维循环是无法收缩成一个点的:
- 一个沿着甜甜圈的“大圈”(环绕甜甜圈的“身体”,通常称为经线 Meridian)。
- 另一个是穿过甜甜圈的“小圈”(环绕甜甜圈的“洞”,通常称为纬线 Longitude)。
- 这两个循环是**$H_1(T^2)$的两个生成元(generators)。因此,我们说$H_1(T^2, \mathbb{Z}) \cong \mathbb{Z} \oplus \mathbb{Z}$(使用整数系数时),它的第一Betti数(First Betti Number)**$b_1(T^2) = 2$,这表示它有两个独立的1-维“洞”。
- 对于甜甜圈表面 ($T^2$),有两个独立的1-维循环是无法收缩成一个点的:
2-1=1维的洞 (1-dimensional dual cycles / “cuts”):
这个概念指的是同调的对偶(dual)概念,即上同调(Cohomology)。直观上,上同调群 $H^k(M)$ 描述了在流形上**$k$-维的“障碍”或“切割”**,这些切割能有效地“分离”流形。- 对于2-维流形上的1-维“洞”($k=1$),它对应的对偶是 $H^{2-1}(T^2) = H^1(T^2)$。
- 您提到“沿着那两个圈把甜甜圈表面切开,而它仍然保持一整片”。这正是对偶的概念:
- 如果你沿着一个纬线(小圈)切割甜甜圈,你会得到一个圆柱体(cylinder),它仍然是连通的。这个切割本身是一条1维的曲线,它是经线同调类的对偶。
- 如果你沿着一个经线(大圈)切割甜甜圈,你也会得到一个圆柱体,同样是连通的。这个切割也是一条1维的曲线,它是纬线同调类的对偶。
- 这两个独立的“切割方式”的数量也是两个。这表明 $H^1(T^2, \mathbb{Z}) \cong \mathbb{Z} \oplus \mathbb{Z}$,它的第一上同调群的秩也是2。
2. 庞加莱对偶性 (Poincaré Duality)
庞加莱对偶性是代数拓扑学中最深刻和优美的定理之一,它连接了流形(manifold)的同调群和上同调群,揭示了流形的内部结构与其边界或“切割”方式之间的深层对称性。
核心思想 (Core Idea):
对于一个闭合(closed)、连通(connected)、可定向(orientable)的 $n$-维流形($n$-manifold)$M$,其$k$-维同调群 $H_k(M)$ 与其 $(n-k)$-维上同调群 $H^{n-k}(M)$ 之间是**同构(isomorphic)**的。
形式化表述 (Formal Statement):
如果 $M$ 是一个闭合、连通、可定向的 $n$-维流形,那么对于任何整数 $k \in {0, 1, \dots, n}$,存在一个同构:
$$H_k(M; G) \cong H^{n-k}(M; G)$$
其中 $G$ 是一个系数群(通常是 $\mathbb{Z}$ 或一个域,如 $\mathbb{R}$)。这个同构是由对偶性配对(Duality Pairing)实现的,通常涉及交叉积(Cap Product)。
关键术语解释 (Key Terminology Explained):
流形 (Manifold):
- 一个拓扑空间,局部看起来像欧几里得空间 $\mathbb{R}^n$。例如,地球表面是2-流形(局部像平面),三维空间中的甜甜圈表面是2-流形(局部像平面),而我们生活的三维空间是3-流形(局部像 $\mathbb{R}^3$)。
- 闭合 (Closed): 紧致(compact)且没有边界(without boundary)。例如,球体表面是闭合的2-流形,圆盘不是(因为它有边界)。
- 可定向 (Orientable): 流形上可以一致地选择一个“方向”或“法线”。例如,球体和甜甜圈表面是可定向的,而莫比乌斯带(Möbius strip)是不可定向的。这是庞加莱对偶性成立的关键条件。
同调群 (Homology Groups, $H_k(M)$):
- 直观概念 (Intuitive Concept): 衡量流形中$k$-维“洞”的数量。它们捕捉到了空间中不可围绕缩小至一点的$k$-维循环。
- 技术定义 (Technical Definition): $H_k(M)$ 是由**$k$-循环($k$-cycles)构成的群模除$k$-边界($k$-boundaries)**构成的群,即 $Z_k/B_k$。
- 0-同调 ($H_0(M)$): 描述连通分支的数量。
- 1-同调 ($H_1(M)$): 描述1-维的“洞”,即无法收缩的环路。对于甜甜圈($T^2$),有2个。
- 2-同调 ($H_2(M)$): 描述2-维的“洞”,即无法填充的空腔。对于甜甜圈($T^2$),有一个(甜甜圈内部的空腔),对于球体($S^2$),也有一个(球体内部的空腔)。
上同调群 (Cohomology Groups, $H^k(M)$):
- 直观概念 (Intuitive Concept): 对偶于同调,通常被认为是测量“障碍”或“切割”的工具。上同调元素可以看作是定义在同调循环上的“函数”或“量度”。
- 技术定义 (Technical Definition): $H^k(M)$ 是由**$k$-上循环($k$-cocycles)构成的群模除$k$-上边界($k$-coboundaries)**构成的群。它们在一定程度上捕捉到了流形如何被“切开”而不分离。
- 0-上同调 ($H^0(M)$): 描述每个连通分支上的常值函数。
- 1-上同调 ($H^1(M)$): 可以看作衡量沿着循环的“流量”或“阻碍”;其元素代表了需要沿着某条曲线放置“墙壁”来分离空间的方式。对于甜甜圈($T^2$),同样有2个独立的这类上同调类。
- 2-上同调 ($H^2(M)$): 对于2-流形,可以看作衡量包裹着“体积”或“区域”的方式。
庞加莱对偶性的例证 (Poincaré Duality in action - Example of a Torus $T^2$):
甜甜圈是一个闭合、连通、可定向的2-维流形 ($n=2$)。让我们看看它的同调群和上同调群(使用整数系数 $\mathbb{Z}$):
$k=0$ (0-维洞 / Connected Components):
- $H_0(T^2; \mathbb{Z}) \cong \mathbb{Z}$ (1个连通分支)
- 根据庞加莱对偶性,应该有 $H_0(T^2; \mathbb{Z}) \cong H^{2-0}(T^2; \mathbb{Z}) = H^2(T^2; \mathbb{Z})$。
- 确实,$H^2(T^2; \mathbb{Z}) \cong \mathbb{Z}$。一个2-维上循环可以看作一个“包裹”整个甜甜圈的表面,对应于它内部的“体积”洞。
$k=1$ (1-维洞 / Loops):
- $H_1(T^2; \mathbb{Z}) \cong \mathbb{Z} \oplus \mathbb{Z}$ (两个独立的环路)
- 根据庞加莱对偶性,应该有 $H_1(T^2; \mathbb{Z}) \cong H^{2-1}(T^2; \mathbb{Z}) = H^1(T^2; \mathbb{Z})$。
- 的确,$H^1(T^2; \mathbb{Z}) \cong \mathbb{Z} \oplus \mathbb{Z}$。这正是您描述的“两种独立的切割方式”。
$k=2$ (2-维洞 / Voids):
- $H_2(T^2; \mathbb{Z}) \cong \mathbb{Z}$ (甜甜圈内部的空腔)
- 根据庞加莱对偶性,应该有 $H_2(T^2; \mathbb{Z}) \cong H^{2-2}(T^2; \mathbb{Z}) = H^0(T^2; \mathbb{Z})$。
- 确实,$H^0(T^2; \mathbb{Z}) \cong \mathbb{Z}$。这再次对应了甜甜圈作为一个整体,只有一个连通分支。
意义 (Significance):
庞加莱对偶性揭示了流形拓扑结构的一种深刻的内在对称性。它表明,流形中$k$-维的“洞”与其对偶的$(n-k)$-维的“切割”或“障碍”之间存在着一一对应的关系。这使得研究高维流形的拓扑性质变得更加容易,因为你可以通过研究其低维的同调或上同调来推断高维的性质,反之亦然。它在微分几何、理论物理(尤其场论)等领域都有广泛应用。
这些例子揭示了,对偶和同构远不止是线性代数的抽象练习。它们是数学家手中的强大工具,能揭示不同领域间惊人的相似性,将一个领域的问题转化到另一个看似无关的领域去解决,并最终展现出数学世界和谐统一的壮丽图景。
